聚类分析实战案例

学习任务

聚类或聚类分析是无监督学习问题。它通常被用作数据分析技术，用于发现数据中的有趣模式，例如基于其行为的客户群。在本章的学习中，您将发现如何在 python 中安装和使用顶级聚类算法。完成本教程后，您将知道：

• 聚类是在输入数据的特征空间中查找自然组的无监督问题。
• 对于所有数据集，有许多不同的聚类算法和单一的最佳方法。
• 在 scikit-learn 机器学习库的 Python 中如何实现、适配和使用顶级聚类算法。

知识点

聚类、聚类分析、亲和力传播算法、Kmeans算法、二分Kmeans算法

1.问题描述

聚类分析简称聚类（clustering），是一个把数据集划分成子集的过程，每一个子集是一个簇（cluster），使得簇中的样本彼此相似，但与其他簇中的样本不相似。

聚类分析不需要事先知道样本的类别，甚至不用知道类别个数，因此它是一种无监督的学习算法，一般用于数据探索，比如群组发现和离群点检测，还可以作为其他算法的预处理步骤。

有许多类型的聚类算法。许多算法在特征空间中的样本之间使用相似度或距离度量，以发现密集的观测区域。聚类方法尝试根据提供给对象的相似性定义对对象进行分组。因此，聚类分析是一个迭代过程，在该过程中，对所识别的群集的主观评估被反馈回算法配置的改变中，直到达到期望的或适当的结果。

以scikit-learn 库为例，它提供了一套不同的聚类算法供选择。

下面列出了10种比较流行的算法：

亲和力传播
聚合聚类
BIRCH
DBSCAN
K-均值
Mini-Batch K-均值
Mean Shift
OPTICS
谱聚类
高斯混合

2.数据模型

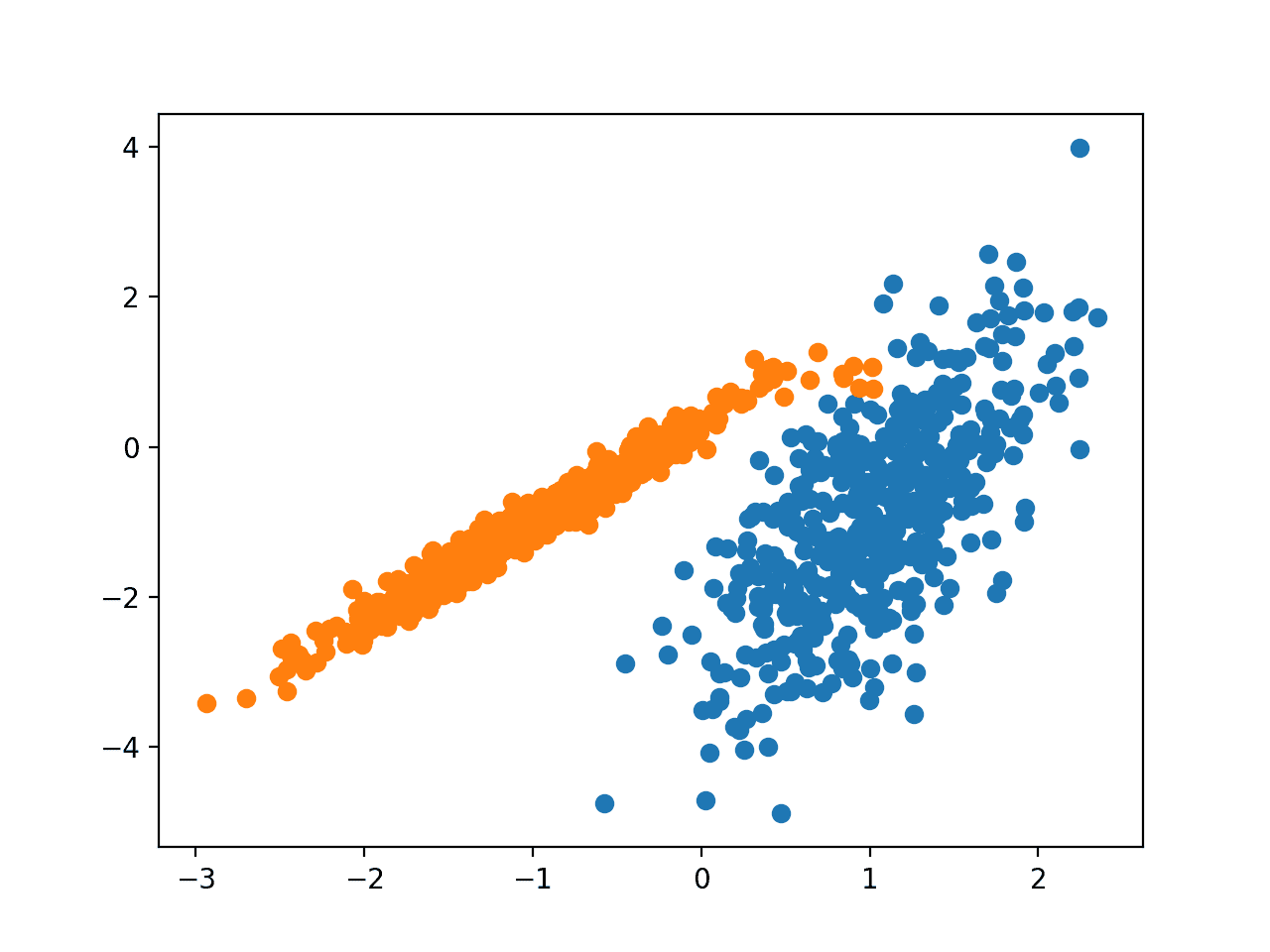
我们将使用 make_classification()函数创建一个测试二分类的数据集。

数据集将有1000个样本，每个类有两个输入特征和一个簇(群集)。很明显，这些群集在二维平面上可见，因此我们可以用散点图绘制数据，并根据不同的群集对图中的点进行上色。这将有助于我们直观地了解群集的识别能力如何。

下面列出了创建和汇总合成聚类数据集的示例。

# 综合分类数据集
from numpy import where
from sklearn.datasets import make_classification
from matplotlib import pyplot
# 定义数据集
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 为每个类的样本创建散点图
for class_value in range(2):
  # 获取此类样本的行索引
  row_ix = where(y == class_value)
  # 创建这些样本的散布
  pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例将创建合成的聚类数据集，然后创建输入数据的散点图，其中点由类标签（理想化的群集）着色。 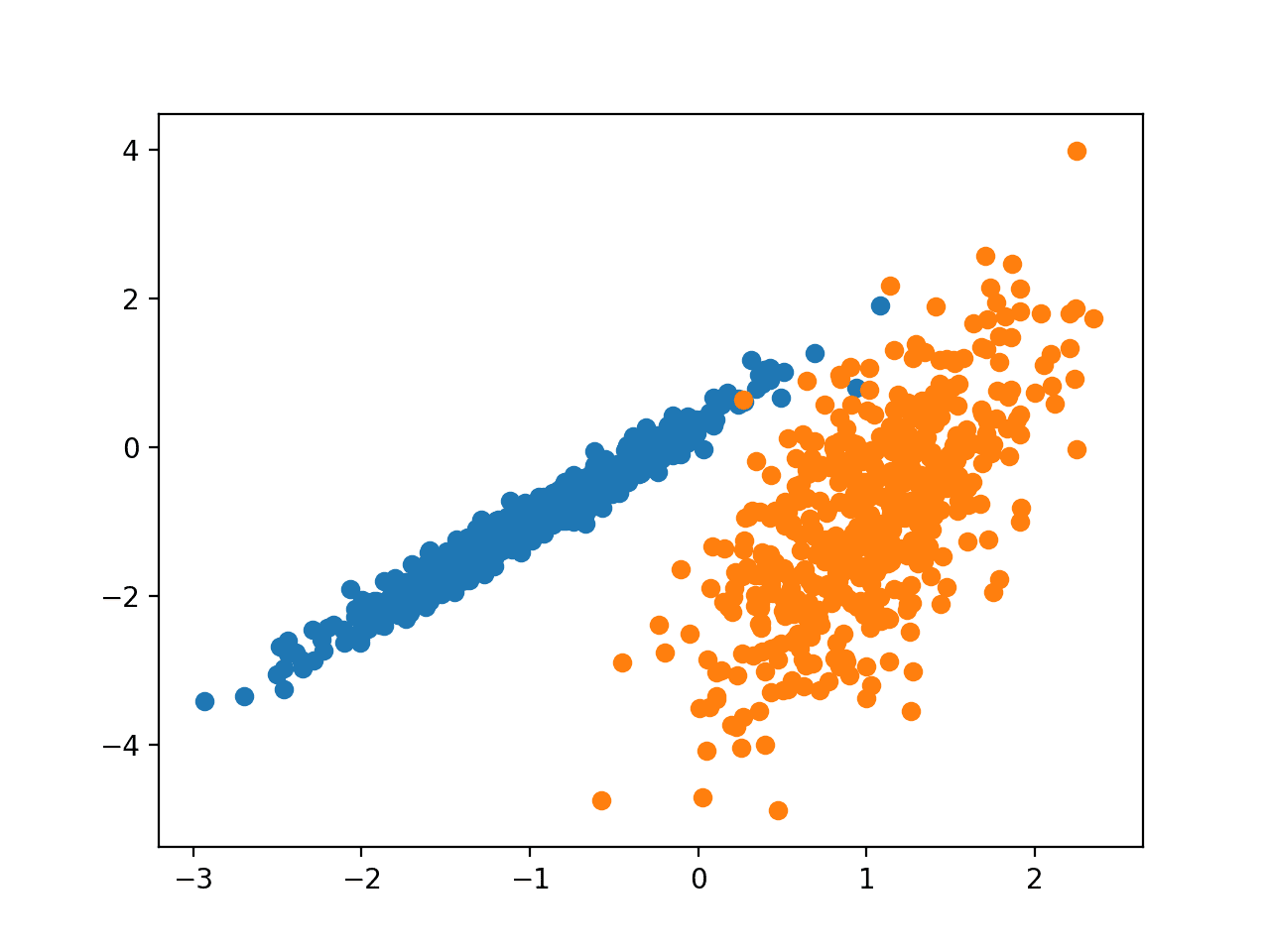我们可以清楚地看到两组不同的数组(分别用蓝色和橙色表示)，接下来的问题是如何使用自动聚类算法来检测出这两个群集。

3.实验过程

3.1 亲和力传播算法

AP(Affinity Propagation)通常被翻译为近邻传播算法或者亲和力传播算法。亲和力传播是指找到一组最能概括数据的范例。AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为exemplar)，然后数据点两两之间连线构成一个网络(相似度矩阵)，再通过网络中各条边的消息(responsibility和availability)传递计算出各样本的聚类中心。

在sklearn中，通过 AffinityPropagation 类实现的，要调整的主要配置是将“阻尼”设置为0.5到1。

下面列出了算法的主要部分：

# 亲和力传播聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AffinityPropagation
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = AffinityPropagation(damping=0.9)
# 训练模型
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
  # 获取此群集的示例的行索引
  row_ix = where(yhat == cluster)
  # 创建这些样本的散布
  pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

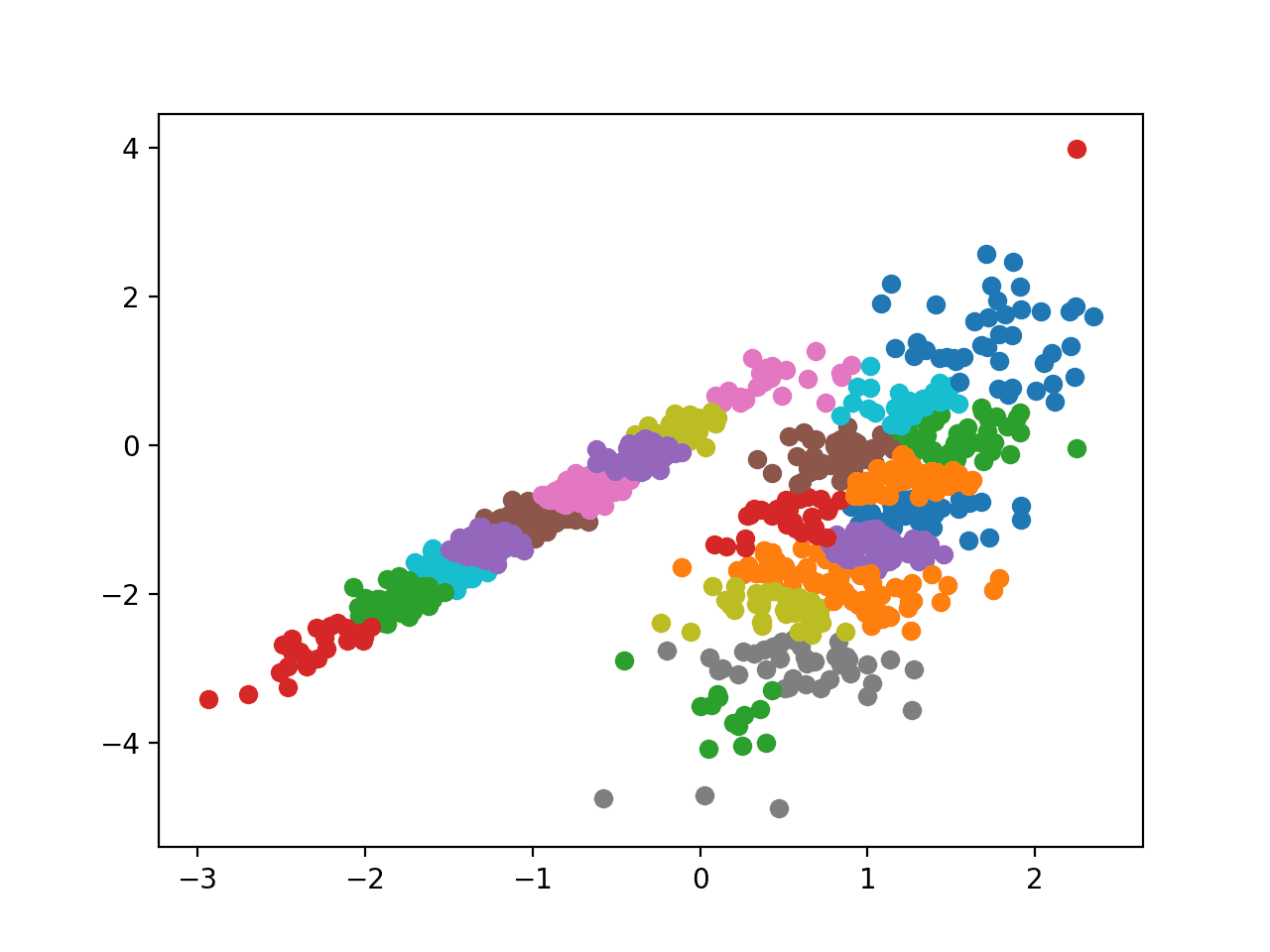
运行程序训练数据集上的模型，并预测数据集中每个样本的群集。然后创建一个散点图，其中的点由指定的群集着色。 在这种情况下，无法找到一个合理的分组。

3.2 BIRCH 算法

BIRCH聚类(BIRCH是Balanced Iterative Reducing and Clustering using Hierarchies平衡迭代缩减和使用层次结构的缩写)，包括构造一个树状结构，从中提取聚类质心。 BIRCH以增量和动态的方式对传入的多维度量数据点进行聚类，以尝试利用可用资源（即可用内存和时间约束）产生最佳质量的聚类。

在sklearn中通过Birch类实现，要调整的主要配置是“threshold”和“n_clusters”超参数，后者提供了群集数量的估计。

下面列出主要代码。

# birch聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import Birch
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = Birch(threshold=0.01, n_clusters=2)
# 训练模型
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
  # 获取此群集的样本的行索引
  row_ix = where(yhat == cluster)
  # 创建这些样本的散布
  pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该程序训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。

在这种情况下，得到了一个很好的结果。

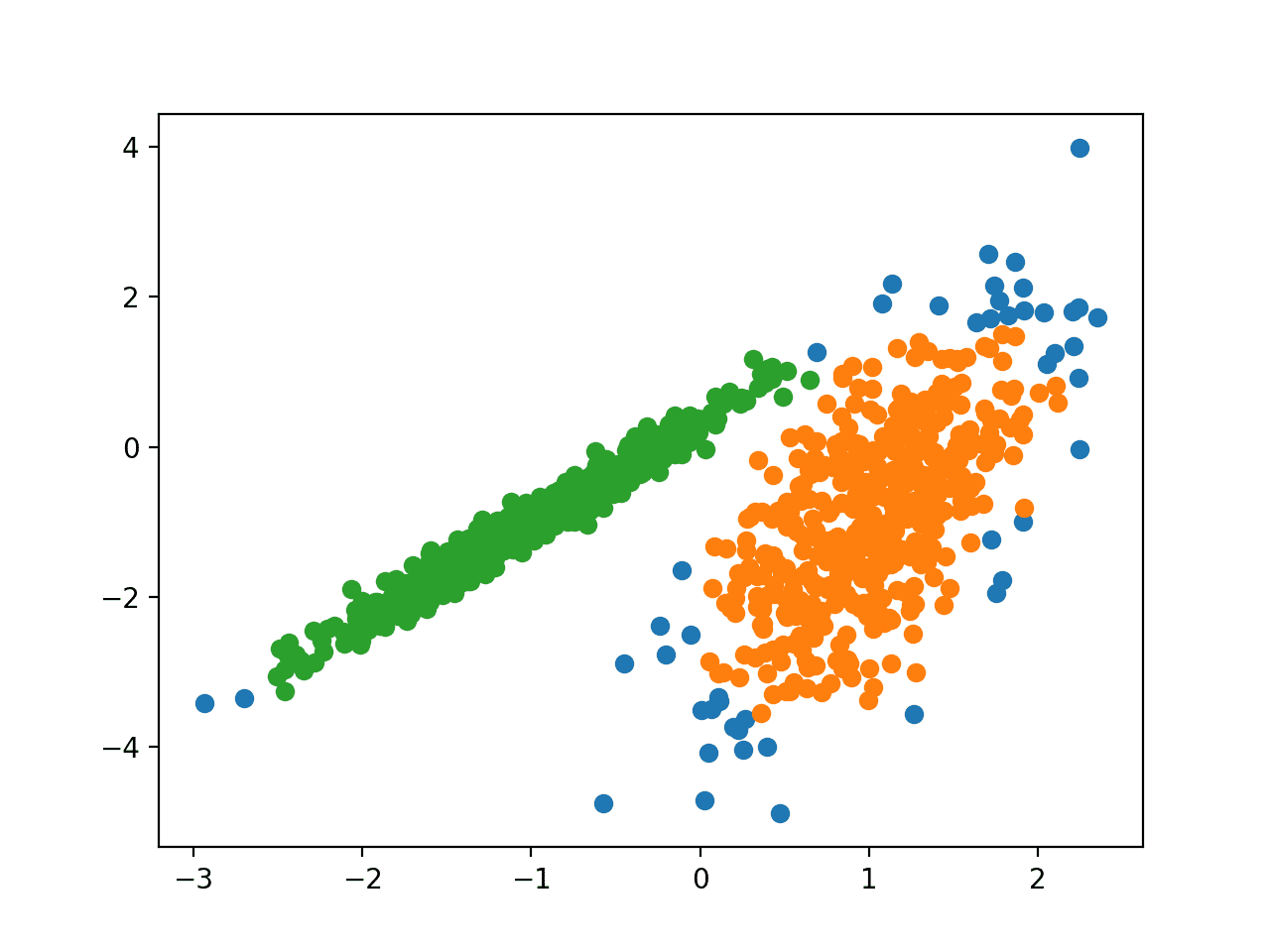
3.3 DBSCAN算法

DBSCAN聚类（DBSCAN是有噪声应用的基于密度的空间聚类的简称）主要是在域中发现高密度区域，并将这些区域周围的特征空间扩展为聚类。

DBSCAN聚类算法，它依赖于基于密度的聚类概念，该概念旨在发现任意形状的聚类。DBSCAN只需要一个输入参数，并支持用户为其确定适当的值

DBSCAN类的实现，要优化的主要配置是“eps”和“min_samples”超参数。

下面列出了完整的示例。

# dbscan聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = DBSCAN(eps=0.30, min_samples=9)
# 训练模型
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
	# 获取此群集的示例的行索引
	row_ix = where(yhat == cluster)
	# 创建这些样本的散布
	pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

在这种情况下，我们可以找到一个合理的分组，尽管可能还需要更多的调整。

3.4高斯混合模型

高斯混合模型概括了一个多变量概率密度函数，顾名思义，它是高斯概率分布的混合。

sklearn是通过GaussianMixture类实现的，要优化的主要配置是“n_clusters”超参数，用于指定数据中估计的群集数量。

下面列出了程序的主要部分。

# 高斯混合模型
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.mixture import GaussianMixture
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = GaussianMixture(n_components=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
  # 获取此群集的示例的行索引
  row_ix = where(yhat == cluster)
  # 创建这些样本的散布
  pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。 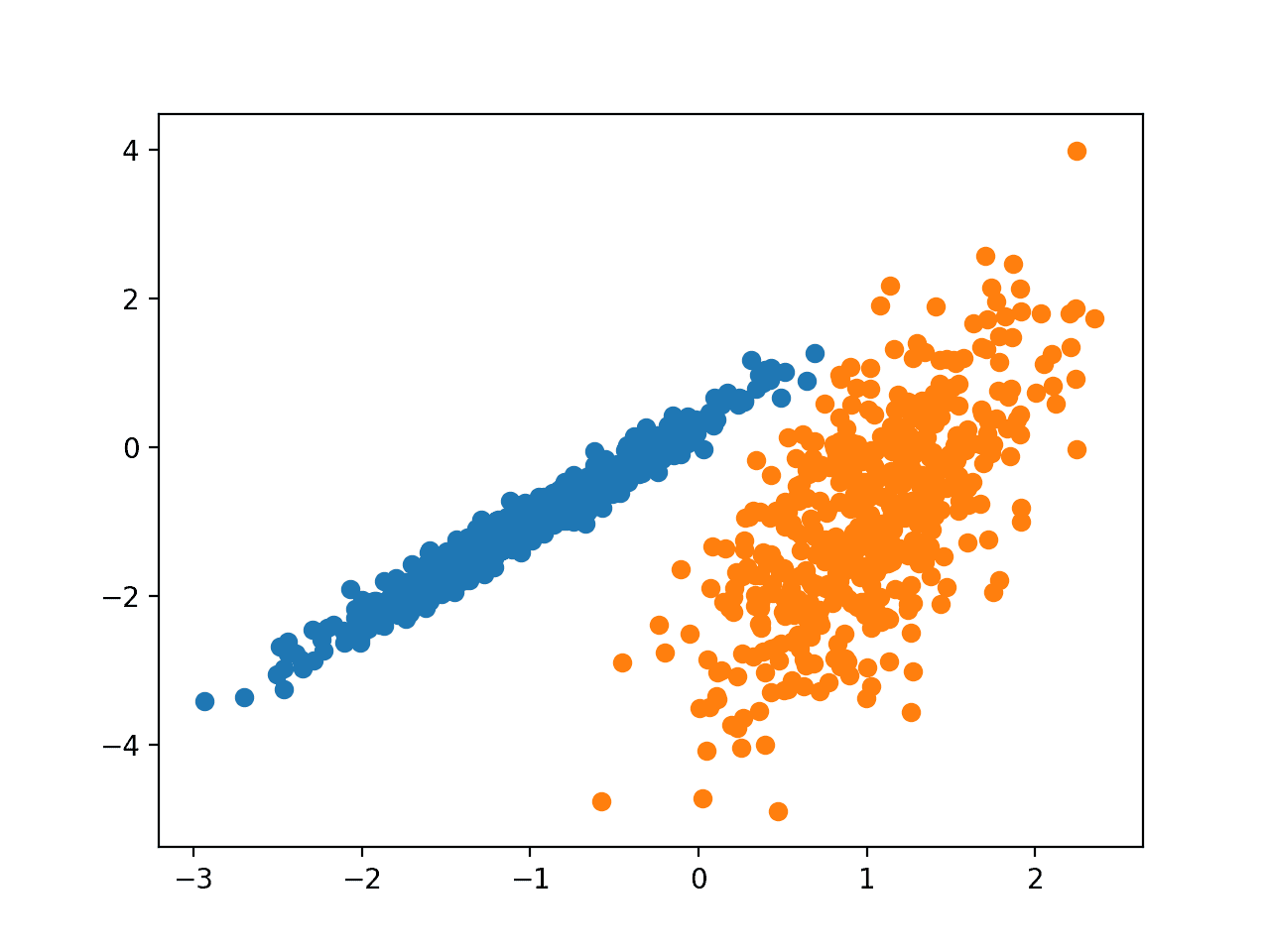在这种情况下，看起来效果非常好。(悄悄说一下，因为数据集就是用高斯混合生成的。)

采用类似的方法，可以编写代码，运行sklearn包中其他的聚类算法。 下面我们看一个稍微复杂的例子，采用二分Kmeans算法对经典手写数字MNIST数据库进行聚类分析。

3.5二分Kmeans算法

首先是数据集的准备，数据文件名为data.pkl，是经典的手写数字MNIST数据库，从中选取1000张（包括0～9共十种数字），用t_sne降到了2维（为了可视化）。

二分Kmeans算法（bisecting Kmeans）是为了克服Kmeans算法收敛于局部最小值的问题而提出的。该算法首先将所有点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值，上述过程不断迭代，直到得到用户指定的簇数目为止。算法步骤如下：

将所有数据点看成一个簇
当簇数目小于k时
       对每一个簇
              计算总误差(sse_origin)
              在给定的簇上面进行k-均值聚类（k=2）
              计算将该簇一分为二后的总误差(sse_new)
       选择使得误差(sse_new)最小的那个簇进行划分操作

根据这个步骤，不难写出二分Kmeans算法的代码，同样地，我们可以将其封装成class，源码如下：

class biKMeans(object):
    def __init__(self,n_clusters=5):
        self.n_clusters = n_clusters
        self.centroids = None
        self.clusterAssment = None
        self.labels = None
        self.sse = None
        
    
    #计算两点的欧式距离
    def _distEclud(self, vecA, vecB):
        return np.linalg.norm(vecA - vecB)
        
    def fit(self,X):
        m = X.shape[0]
        self.clusterAssment = np.zeros((m,2))
        centroid0 = np.mean(X, axis=0).tolist()
        centList =[centroid0]
        for j in range(m):#计算每个样本点与质心之间初始的平方误差
            self.clusterAssment[j,1] = self._distEclud(np.asarray(centroid0), X[j,:])**2
        
        while (len(centList) < self.n_clusters):
            lowestSSE = np.inf
            for i in range(len(centList)):#尝试划分每一族,选取使得误差最小的那个族进行划分
                ptsInCurrCluster = X[np.nonzero(self.clusterAssment[:,0]==i)[0],:]
                clf = KMeans(n_clusters=2)
                clf.fit(ptsInCurrCluster)
                centroidMat, splitClustAss = clf.centroids, clf.clusterAssment#划分该族后，所得到的质心、分配结果及误差矩阵
                sseSplit = sum(splitClustAss[:,1])
                sseNotSplit = sum(self.clusterAssment[np.nonzero(self.clusterAssment[:,0]!=i)[0],1])
                if (sseSplit + sseNotSplit) < lowestSSE:
                    bestCentToSplit = i
                    bestNewCents = centroidMat
                    bestClustAss = splitClustAss.copy()
                    lowestSSE = sseSplit + sseNotSplit
            #该族被划分成两个子族后,其中一个子族的索引变为原族的索引，另一个子族的索引变为len(centList),然后存入centList
            bestClustAss[np.nonzero(bestClustAss[:,0] == 1)[0],0] = len(centList)
            bestClustAss[np.nonzero(bestClustAss[:,0] == 0)[0],0] = bestCentToSplit
            centList[bestCentToSplit] = bestNewCents[0,:].tolist()
            centList.append(bestNewCents[1,:].tolist())
            self.clusterAssment[np.nonzero(self.clusterAssment[:,0] == bestCentToSplit)[0],:]= bestClustAss 
                   
        self.labels = self.clusterAssment[:,0] 
        self.sse = sum(self.clusterAssment[:,1])
        self.centroids = np.asarray(centList)
                                
    def predict(self,X):#根据聚类结果，预测新输入数据所属的族
        #类型检查
        if not isinstance(X,np.ndarray):
            try:
                X = np.asarray(X)
            except:
                raise TypeError("numpy.ndarray required for X")
        
        m = X.shape[0]#m代表样本数量
        preds = np.empty((m,))
        for i in range(m):#将每个样本点分配到离它最近的质心所属的族
            minDist = np.inf
            for j in range(self.n_clusters):
                distJI = self._distEclud(self.centroids[j,:],X[i,:])
                if distJI < minDist:
                    minDist = distJI
                    preds[i] = j
        return preds

该类的使用方法如下:

import numpy as np
import matplotlib.pyplot as plt
from kmeans import biKMeans
n_clusters = 10
clf = biKMeans(n_clusters)
clf.fit(X)
cents = clf.centroids
labels = clf.labels
sse = clf.sse
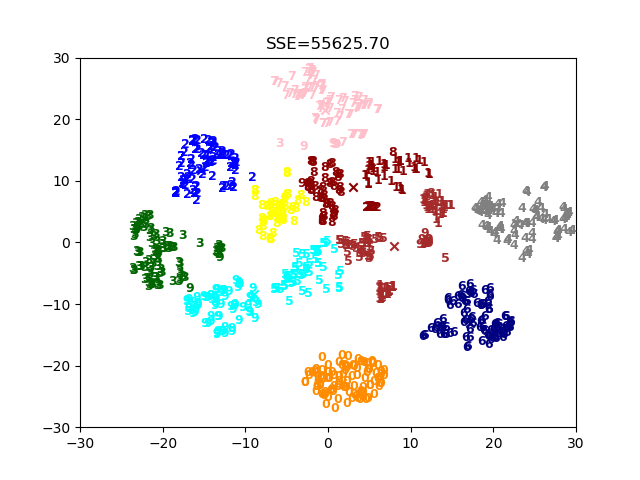
#画出聚类结果，每一类用一种颜色
colors = ['b','g','r','k','c','m','y','#e24fff','#524C90','#845868']
for i in range(n_clusters):
    index = np.nonzero(labels==i)[0]
    x0 = X[index,0]
    x1 = X[index,1]
    y_i = y[index]
    for j in range(len(x0)):
        plt.text(x0[j],x1[j],str(int(y_i[j])),color=colors[i],\
                fontdict={'weight': 'bold', 'size': 9})
    plt.scatter(cents[i,0],cents[i,1],marker='x',color=colors[i],linewidths=12)
plt.title("SSE={:.2f}".format(sse))
plt.axis([-30,30,-30,30])
plt.show()

运行程序，可以得到类似下图的结果。

多次运行上面的代码，结果可能都是不一样的，这是因为二分Kmeans算法在“二分”的时候，采取的也是随机初始化质心的方式。

4.小结

在本教程中，您学习了如何在 python 中安装和使用顶级聚类算法。以上所有的算法的实现都是依赖于机器学习库—scikit-learn库，当然还有其他聚类比如，谱聚类，Apriori关联分析等都有很好的聚类分析能力。只要掌握其思想，才能对各种聚算法融会贯通。